熱交換器の効率ってどうやって計算するの？
熱交換器の設計にどう使うの？
そんな悩みを解決します。
・熱交換器の温度効率の計算方法
・温度効率を用いた熱交換器の設計例
この記事を読めば、熱交換器の温度効率を計算し、熱交換器を設計する基礎が身に付きます。
私の仕事は化学プラントの設計です。
その経験をもとに分かりやすく解説します。
☑ 化学メーカー生産技術職
☑ 工学修士（専攻：化学工学）
熱交換器の温度効率の計算方法
熱交換器の性能は二つの視点から評価されます。
- 熱交換性能
高温流体から低温流体へどれだけの熱エネルギーを移動させられるか - 温度交換性能
高温流体と低温流体の温度をどれだけ変化させられるか
①熱交換性能は全交換熱量Qを求めれば良く、総括伝熱係数U、伝熱面積A、対数平均温度差ΔTlmから求められます。
$$Q=UAΔT_{lm}$$
Q：全交換熱量［W］
U：総括伝熱伝熱係数［W/m2·K］
A：伝熱面積［m2］
ΔTlm：対数平均温度差［K］
詳細は以下の記事で解説しています。
総括伝熱係数とは？求め方と計算例
熱交換器の伝熱面積の求め方【熱交換器の計算例】
一方②温度交換性能（高温流体と低温流体の温度をどれだけ変化させられるか）を評価するとき「温度効率」という指標が用いられます。
ここから温度効率について分かりやすく解説していきます。
熱交換器の温度効率の計算式
熱交換器の温度効率を計算する方法は２パターンあります。
- 流体の出入口温度から求める方法
- 熱容量流量比Rhと伝熱単位数Nhを用いる方法
流体の入口温度、出口温度が分かるときは以下の式から温度効率を求めることができます。
温度効率の計算式は、熱交換器で達成できる最大の温度降下または温度上昇に対して、実際の温度降下や温度上昇の割合を示しています。
高温流体側温度効率
$$φ_h=\frac{T_{hi}−T_{ho}}{T_{hi}−T_{ci}}・・①$$
低温流体側温度効率
$$φ_h=\frac{T_{co}−T_{ci}}{T_{hi}−T_{ci}}・・②$$
φ：温度効率［ー］
T：流体温度［K］
添え字
h：高温側流体
c：低温側流体
i：入口
o：出口
流体出口温度が未知のとき、熱容量流量比Rhと伝熱単位数Nhを用いて、以下の式から温度効率を計算できます。
並流型熱交換器
$$φ_h=\frac{1−exp(−N_h(1+R_h))}{1+R_h}・・③$$
$$φ_c=R_hφ_h・・④$$
向流型熱交換器
$$φ_h=\frac{1−exp(−N_h(1−R_h))}{1−R_hexp(−N_h(1−R_h))}・・⑤$$
$$φ_c=R_hφ_h・・⑥$$
熱容量流量比Rhと伝熱単位数Nhは以下の式から求めます。
$$R_h=\frac{m_hc_h}{m_cc_c}・・⑦$$
$$N_h=\frac{UA}{m_hc_h}・・⑧$$
m：質量流量［kg/s］
c：比熱［J/kg·K］
添え字
h：高温側流体
c：低温側流体
伝熱単位数Nhは高温流体の熱容量流量に対する隔板の熱通過の良さを表しています。
直行流型熱交換器やシェルアンドチューブ型熱交換器など、並流型·交流型熱交換器以外の熱交換器の場合、補正係数ψを用いて計算できます。
$$φ_h=\frac{1−exp(−ψN_h(1−R_h))}{1−R_hexp(−ψN_h(1−R_h)}$$
$$φ_c=R_hφ_h$$
直行流型熱交換器やシェルアンドチューブ型熱交換器などの熱交換器の高温側·低温側流体間の平均温度差は厳密には対数平均温度差では表せず、補正する必要があるためです。
$$ΔT_{lm}=ψΔT_{lm}$$
補正係数ψは化学工学便覧や伝熱工学の参考書で調べることができます。
並流型と交流型の温度効率の比較
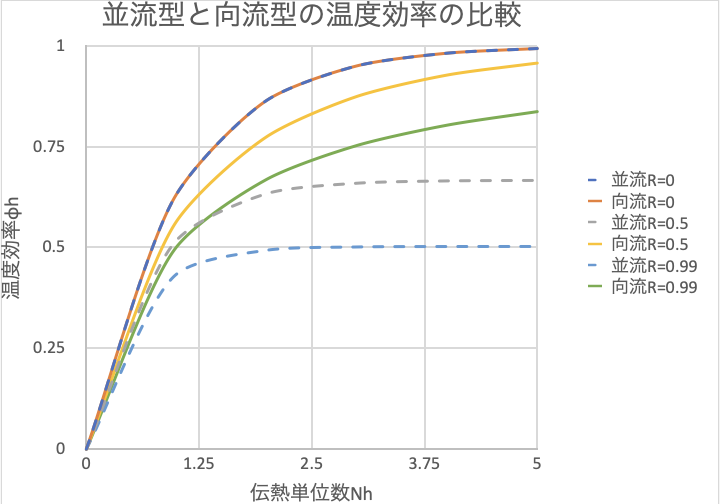
並流型（式③）と向流型（式⑤）を比較すると、向流型の方が温度効率が良いことが分かります。
これが向流型の方が効率が良いと言われる理由です。
温度効率を用いた熱交換器の設計例
温度効率を用いた熱交換器の設計例をご紹介します。
以下の設計条件から、温度効率を計算して両流体出口温度を求め、最終的には交換熱量を算出します。
設計条件
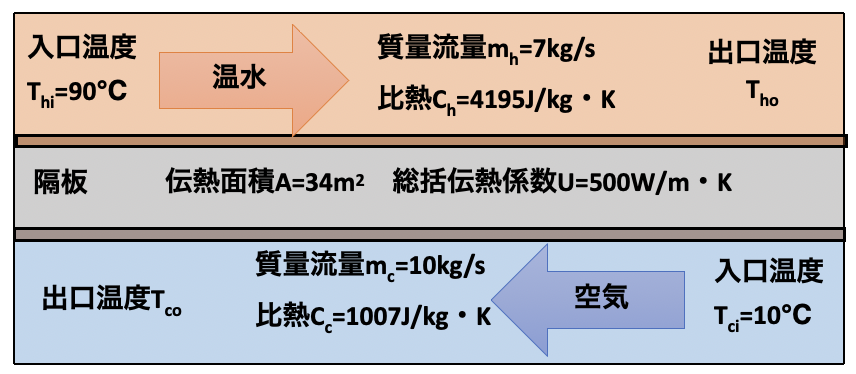
・向流型熱交換器、伝熱面積A=34m2、総括伝熱係数U=500W/m·K
・高温側流体：温水、Thi=90℃、mh=7kg/s、Ch=4195J/kg·K
・低温側流体：空気、Tci=10℃、mc=10kg/s、Ch=1007J/kg·K
①熱容量流量比Rhを求める
$$R_h=\frac{m_hc_h}{m_cc_c}・・⑦$$
$$=\frac{7×4195}{10×1007}$$
$$=2.196$$
②伝熱単位数Nhを求める
$$N_h=\frac{UA}{m_hc_h}・・⑧$$
$$=\frac{500×34}{7×4195}$$
$$=0.579$$
③温度効率φを求める
高温流体側の温度効率は
$$φ_h=\frac{1−exp(−N_h(1−R_h))}{1−R_hexp(−N_h(1−R_h))}・・⑤$$
$$=\frac{1−exp(−0.579(1−2.196))}{1−2.196exp(−0.579(1−2.196))}$$
$$=0.295$$
低温流体側の温度効率は
$$φ_c=R_hφ_h・・⑥$$
$$=2.196×0.295$$
$$=0.647$$
④流体出口温度を求める
高温流体側出口温度は
·$$φ_h=\frac{T_{hi}−T_{ho}}{T_{hi}−T_{ci}}・・①$$
$$T_{ho}=T_{hi}−φ_h(T_{h}I−T_{ci})$$
$$=90−0.295(90−10)℃$$
$$=66.4℃$$
低温側流体出口温度は
$$φ_h=\frac{T_{co}−T_{ci}}{T_{hi}−T_{ci}}・・②$$
$$T_{co}=T_{ci}+φ_c(T_{hi}−T_{ci})$$
$$=10+0.647(90−10)℃$$
$$=61.8℃$$
⑤対数平均温度差Tlmを求める
$$ΔT_{lm}=\frac{(T_{hi}−T_{co})−(T_{ho}−T_{ci})}{lnT_{hi}−T_{co}T_{ho}−T_{co}}$$
$$ΔTlm=\frac{(90−61.8)−(66.4−10)}{ln\frac{90−61.8}{66.4−10}}$$
$$=40.7K$$
全交換熱量Qを求める
$$Q=UAΔT_{lm}$$
$$=500×34×40.7$$
$$=6.92×10^5W$$
まとめ
熱交換器の温度効率の計算方法と温度効率を用いた設計例を解説しました。
直行流型熱交換器やシェルアンドチューブ型熱交換器など、並流型·交流型熱交換器以外の熱交換器の場合、補正係数ψを用いて計算できます。
より深く学びたい方には、参考書で体系的に学ぶことをおすすめします。
初学者におすすめの伝熱工学の参考書６選！
