真空排気のコンダクタンスってどうやって求めるの?
そんな悩みを解決します。
様々な配管のコンダクタンスの求め方
①長い円形配管
②短い円形配管
③曲がり管とエルボ
この記事を読めばコンダクタンスの意味を理解し、様々な配管についてコンダクタンスを求められるようになります。
真空排気の設計方法については「真空ポンプの排気速度と配管径の求め方」で解説しています。

私の仕事は化学プラントの設計です。
その経験をもとに分かりやすく解説します。

様々な配管のコンダクタンスの求め方
コンダクタンスK[m3/s]は流体の流れやすさを表す指標であり、流動抵抗の逆数に相当します。
配管の両端における圧力差をp1−p2とすれば、以下の式となります。
Q:真空排気量[m3・Pa/s]
p1−p2:圧力差[Pa]
圧力損失が大きくなるほど、コンダクタンスは小さくなります。
「コンダクタンスは数値が大きいほど流体が流れやすく、小さいほど流れにくい」という感覚を持ってくださいね。
設計段階で圧力差p1−p2はわからないため、以下のようにコンダクタンスを計算します。
排気系全体のコンダクタンスは、K1,K2,K3,・・・の配管が直列にあるとき
並列にあるとき
K1,K2,K3,・・・は以下のように場合分けして求める。
長い円形配管のコンダクタンス(l>d)
この先共通の記号を先に示しておきます。
<共通記号>
d:配管内径[m]
l:配管長さ[m]
p:圧力の算術平均値[Pa]
μ:流体粘度[kg/(m・s)]
T:流体温度[K]
M:分子量[g/mol]
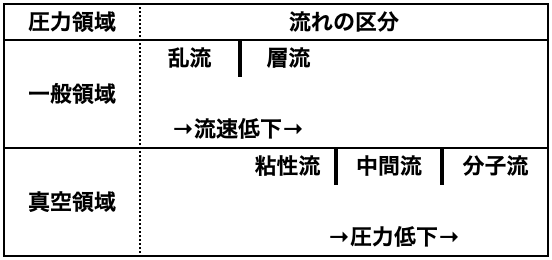
ここで、λmは
λm:気体分子の平均自由行路[m]
λm0:273K,133PAにおける気体分子の平均自由行路[m]
λm0は以下に示す。
| 気体 | 空気 | H 2 | O 2 | C O 2 |
| λ m 0 × 105 | 4.54 | 8.37 | 4.81 | 2.95 |
短い円形配管のコンダクタンス(l≦d)
長い円形配管のコンダクタンスkvlを補正して
長い円形配管のコンダクタンスKmlの式のlの代わりに以下を用いる。
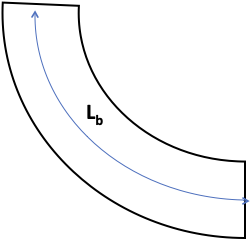
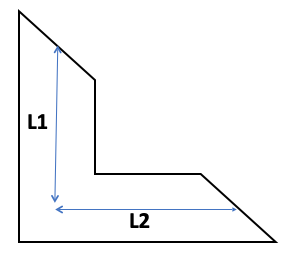
曲がり管とエルボのコンダクタンス
上記の式の長さlに相当長さleを用いる。
曲がり管の相当長さは
lc:中心線長さ[m]
まとめ
様々な配管のコンダクタンスの求め方を解説しました。
コンダクタンスは真空排気の設計において必ず求めなければならないものです。
コンダクタンスの意味を理解し、状況に応じて適切に求められるようにしましょう。
真空技術をもっと勉強したい方は、参考書で体系的に学ぶのがおすすめです。
 初学者におすすめの真空技術の参考書5選!
初学者におすすめの真空技術の参考書5選!